

- 您好,欢迎您访问成贯仪器官方网站!


术语镜片是赋予玻璃或透明塑料材料制成的部件,通常在直径的圆形,它有两个主表面,在设计,以产生一个会聚或通过的光的发散的特定方式是研磨和抛光的通用名材料。 光学显微镜通过从照明器通过一系列的玻璃透镜在传统摄像系统使光与该光聚焦或进入目镜,在薄膜平面形成放置在台上的检体的图像,或者上的一个表面数字图像传感器。

一个简单的镜头,类似于许多那些在显微镜使用的作用,是通过折射和反射的原则支配,可以用几个简单的规则所涉及的通过镜头光线跟踪几何形状的援助来理解。 在此讨论探讨的基本概念,这是从几何光学的科学衍生,将导致放大过程的理解,实际和虚拟图像,以及透镜像差或缺陷的性质。
为了了解一个简单的显微镜的光学系统(在一个共同的实验室显微镜透镜元件的位置在图1中),具有两个光折射的表面和中心光轴必须首先简单薄透镜的基本性能进行说明。 每个透镜有两个主平面和由该透镜的几何形状和透镜和聚焦图像之间的关系定义了两个焦平面 。 光线通过透镜将交叉并在焦平面(见图2)在物理上是统一,而进入透镜的光线的扩展将在主平面相交的光线从透镜新兴的扩展。 透镜的焦距定义为主要平面和焦平面之间的距离,并且每一个透镜具有一组在每一侧(前和后)这些平面。
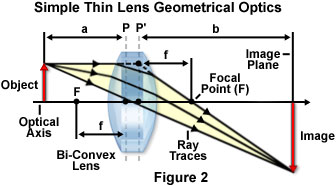
的穿过一个简单的双凸薄板玻璃透镜的光线迹线示于图2中,具有必要在形成由射线聚焦图像的其它重要几何参数。 透镜的焦点由变量f表示,并且有两个独立的联络点,一个在透镜(在 图2的左手侧)的正面,一个位于透镜(在 右侧)的后面。 透镜(P和图2中的P')的主面用虚线表示,并且每一个主平面和其相应的焦点之间的距离表示焦距(f)。 因为在图2所示的双凸透镜是对称的,所述主面位于距透镜表面相等的距离,并且前部和后部的焦距也相等。
由透镜所成像的对象(或检体)被定位在物体面 ,位 于按照惯例透镜的左手侧,并且由一红色箭头从中心线或光轴 ,它传递向上行进表示通过透镜的中心,垂直于主平面。 射线通过透镜(黄色箭头)跟踪从对象发出,并从通过透镜从左到右以在该透镜的右侧在图像平面上的放大的实图像(反转红色箭头)进行。 透镜的前侧主平面与样品之间的距离是已知的作为对象的距离 ,并且由可变一在图2中表示。在一个类似的方式,从后方主平面到图像的距离(变量b在图2中)被称为图像距离 。 这些参数定义一个简单的透镜的几何光学的基本元件,并且可以被用来计算透镜的重要特性,包括焦距和放大倍数。
透镜可以根据它们是否会导致光线穿过会聚成一个单一的聚焦点,或从光轴并进入空间向外岔开为正或负 。正透镜(在图2和3示出)会聚入射光线是平行于光轴和聚焦它们在焦平面,以形成一个实象。 如在图3中所示,正透镜具有一个或两个凸表面,并且在中心比边缘厚。 的正透镜的一个共同特点是,它们放大物体时它们被放置在物体与人眼之间。 与此相反,负透镜发散平行入射光线并通过延伸通过透镜传递到透镜后面的焦点的光线痕迹形成的虚像。 负透镜具有至少一个凹面,并且在中心比边缘薄(参见图3)。 当负透镜被置于一个物体和眼睛之间,它不会形成真正的图像,但通过形成的虚像减少(或缩小)对象的表观大小。
通过一透镜或反射镜系统成像的标本时,不管系统是否由单个或多个组件的一个实部和一个虚像之间的区别是一个重要的概念。 在一般情况下,图像通过其中,光线(及其附加信息)成为会聚作为由反射镜的透镜或反射折射的结果的区域来定义。 在那里的光线相交于焦点的情况下,图像是真实的,可以在一个屏幕上观看,记录在胶片上,或投射到传感器的表面上,如放置在图像平面上的CCD或CMOS。 当光线发散,但是预计,会聚到一个焦点假想扩展,该图像是虚拟的,不能在屏幕上观看或记录在胶片上。 在待可视化顺序,必须在眼睛的视网膜上形成的实像。 当通过显微镜的目镜观看标本,形成在视网膜上的实像,但实际上是由观察者察觉到存在为位于约10英寸(25厘米)在眼睛前面的虚拟图像。
在图3所示的正透镜元件的主透镜的几何形状是双凸 (图3(a))和平凸透镜 (图3的(b);具有一个平面或平坦的表面)。 此外, 凸弯月面 (图3(c))的透镜具有相似曲率既凸面和凹面,但是在中心比边缘厚。双凸透镜是最简单的放大镜,并且有一个焦点和倍率是依赖于表面的曲率角度。 曲率导致较短的焦距更高的角度,由于这样的事实,光波以更大的角度折射相对于该透镜的光轴。 双凸透镜的对称性质最小化在图像和对象的位置对称地应用球面像差。 当双凸的光学系统是完全对称(实际上,1:1的放大率),球面象差是在最小值和彗差和失真都同样最小化或取消。 一般情况下,双凸透镜与0.2倍和5倍的放大倍率最小畸变执行。 凸透镜主要用于聚焦应用和图像放大率。
典型平凸透镜(如图3(b))具有一个正凸面并在透镜的另一侧的平坦(平)面。 这些透镜元件聚焦平行光线到一个焦点是正并形成可以投射或通过空间滤波器操纵的真实图像。 平凸透镜的不对称性的应用中最小球面象差,其中所述对象和图像谎言在离透镜距离不等。 当对象被放置在无穷大(实际上,平行光线进入透镜)与图像是最后的聚焦点发生减少象差的最佳的情况。 然而,平凸透镜会产生在共轭比率高达约5最小像差:1。 当平凸透镜的曲面朝向面向对象,最清晰可能的焦点来实现的。 平凸透镜是用于准直发散光束并施加聚焦到一个更复杂的光学系统是有用的。
正弯月形透镜(如图3(c))具有成形为凸半径一面不对称结构,而相反的面是稍凹。 弯月形透镜经常被一起使用与另一种透镜,以产生具有或者较长或较短焦距比原始透镜的光学系统。 作为一个例子,一个正凹凸透镜可以位于一个平凸透镜后缩短焦距不降低光学系统的性能。 正弯月形透镜具有在透镜比在凸侧的凹侧更大的曲率半径,使形成实像。
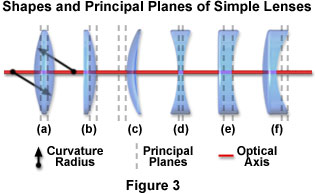
负透镜元件是双凹 (图3(d))的, 平凹 (图3(E);具有一个平坦表面),以及凹弯月 (图3(F)),其也具有凹部和凸面,但与镜片比边缘薄的中心。 对于正的和负弯月形透镜,表面和其焦平面之间的距离是不相等的,但它们的焦距相等。 连接透镜曲面的中心图3中的线被称为透镜的光轴。 具有对称形状(双凸或双凹)简单透镜具有主面,由虚线在图3中,也同样相对于间隔开,彼此透镜表面表示。 两个凸面的双凸透镜的曲率半径是由黑色箭头在图3(a)所示。 缺乏其他镜片,如弯月形透镜与平负和正透镜对称的,使主面的位置根据镜头的几何形状而变化。 平凸和平凹镜片具有相交的光轴,在弯曲表面的边缘一个主平面,和埋在玻璃内的其它平面上。 为凹凸透镜的主平面趴在透镜表面之外。
双凹透镜(图3(d))的主要用于发散光束和图象尺寸减小,以及增加光学系统的焦距和准直会聚光束。 通常被称为双凹透镜 ,该光学元件折射并行输入光线,使它们发散从在透镜的输出侧的光轴远离,形成在透镜前面的负焦点。 尽管输出的光线实际上不凝聚,以形成一个焦点,它们似乎是从位于透镜的物体侧的虚像发散。 双凹透镜可耦合到其它透镜,以减少光学系统的焦距。
在图3(e)所示的平凹透镜是具有负光焦点,并产生一个虚拟图象的发散元件。 当准直光束入射到平凹透镜元件的弯曲表面上,出射侧将形成发散的光束。 该光束将出现从一较小的虚拟点声源出现比如果平面透镜表面已经面临的准直光束。 平凹镜片,其中设有最小球面像差时的凹面朝向最长共轭距离,被用来扩大光束或增加现有的光学系统的焦距。
也称为凹凸透镜,负(发散)弯月形透镜可以被设计成减少或消除额外的球面像差或彗差的光学系统,以使透镜耦合。 弯月形透镜(正面和负面)通常用于缩短双峰(两个透镜元件胶合在一起)或平凸透镜在无限共轭比操作的焦距(由平行光线照射)。 最终系统的期望焦距确定应添加的弯月形透镜的特定尺寸和字符。 平凸/凹凸透镜组合显示高达四倍比平凸透镜单独工作时更高的分辨率。
透镜由在它们进入和退出透镜面分折射入射光波前进行操作。 折射的角度,因此,焦距,将取决于所述透镜表面的几何形状以及用于构造透镜的材料。 与折射指数高的材料将具有更短的焦距比低的折射率。 例如,镜片由合成聚合物,如有机玻璃(1.47折射率),具有比玻璃(1.51)更低的折射率导致稍长焦距。 幸运的是,璐彩特和玻璃的折射率是如此接近在一起璐彩特可代替玻璃在许多镜头的应用,其中包括正在享受深受广大消费者的使用流行的电影,在一箱相机中使用。 由纯金刚石(2.42折射率)的透镜将具有的焦距比玻璃或有机玻璃显著以下,虽然纯净的钻石的高成本会望而却步透镜构造。
如上所述,所有透镜具有与该透镜的前和后表面相关联的两个主平面。 在显微镜,透镜经常胶合在一起以形成更大的基团( 厚透镜)具有相对于该透镜面的主面相当不寻常的位置。 然而,不管透镜元件的数量或透镜系统的复杂性,在主平面的厚透镜的位置可以通过透镜的精确附图光线跟踪确定。 现代透镜设计和光学工程师使用复杂的计算机程序来模拟,设计,并通过各个透镜和多元件透镜系统追踪光线。 这些软件程序用于设计照相机,望远镜,显微镜,并依赖于玻璃(或塑料)的镜头形成图像的其他光学器件。
有适用于通过简单的透镜光线跟踪三个一般规则(见图2),这使任务相对简单。 首先,光线通过透镜的中心从物体上的点到相应的点处的图像(箭头的图2中的前端部)上绘制。 此射线不被透镜偏离。 其次,从对象的最上点发出的光线平行勾勒于光轴并且,由透镜折射后,将相交并穿过后方焦点。 事实上,这是于光轴行进平行所有光线将被透镜折射后通过后方焦点。 第三,从通过前焦点的对象的光线将通过在一个方向上的透镜平行于光轴并与所述图像上的相同点一致被折射。 刚才所描述的射线,这通常被称为特征射线中的任何两个的交点,将定义透镜的像平面上。
延伸个别光线轨迹的概念来的光束是必要描述在显微镜中发生的光学事件。 当光的平行光束通过一个简单的透镜,光线被折射,并浓缩成光的聚焦光点在焦点处(点F在图2中)的镜头。 另外,当从位于一个透镜的焦点处的点光源的光进入透镜,它出现光的近轴,平行光束。 从显微镜照明源的光可被认为是光波在相位彼此振动的一列火车。 与此波列相关联的波阵面在于垂直于传播方向的平面(通常平行于显微镜的光轴),并且当通过一个简单的双凸透镜传递被转换成球面波。 球形波的半径在镜头的焦点中心,和光波所有到达阶段,在焦点处相互进行建设性的(添加剂)的干扰。 作为为光的点光源的情况下,从一个简单的透镜的焦点发出的球面波前转换成由折射平面波阵面通过透镜时发生。
A面波前通过空间行进往往不是垂直于透镜的光轴的,而是在发生率的某些角度即从轴线倾斜到达。 球面波通过镜头从离轴平面波的通路导致的中心位于在某个点从透镜的光轴离开。 对于所有的实际物镜,平面波可被认为是无限大的半径,这可以通过一个透镜被聚焦成具有更小的半径是等于透镜的焦距的另一球面波的球面波。 因此,可以得出结论,一个简单的双凸透镜被一个球面波转换成另球面波,常常使用不同的半径(或焦点)进行操作。 此外,第二球面波的曲率中心位于透镜的焦平面上。
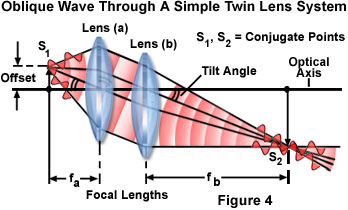
如果发光球面波点光源不会在透镜的焦平面位于(在实际上,光波是倾斜于光轴),透镜可以被描述为包括两个分离的透镜,如图4所示为一红色单色(单一颜色)的点源。 每个透镜具有不同的焦距(f(a)用于在透镜最近的图4和f(b)在所述第二透镜的点光源),并从第二透镜出现的球面波(透镜(b))的是在焦点,它也从该透镜系统的光轴除去居中。 其结果是,(1)在图4中S点为中心的球面波被第一透镜转换成由相同的角作为点源倾斜相对于该透镜轴线的平面波。 第二透镜转换的平面波从第一透镜新兴成具有在点S(2),其也被倾斜以相同的角度为点源为中心的一个曲率半径的另一球面波。 总之,简单的透镜(这是如在图4中描述的两个假设组分透镜的总和)的重点点源S(1)到S点(2)和反之亦然。 在光学方面,点S(1)和S(2)被称为共轭点 ,并且根本重要性在显微镜的光学列车发生理解的事件。
至位进一步延伸共轭点的想法,如果点S(1)被认为是属于一组位于在垂直于透镜的光轴的平面的点,则透镜将每个点聚焦到含有点集S的平面中类似共轭点(2)。 因此,通过对等,透镜也将在平面S(2)的每个点上聚焦从原始平面集合S(1)相应的点。 这些紧密相关的焦平面被称为共轭平面 ,并在同时的焦点。 在一般情况下,在显微镜有两组共轭面的:一种包含通过光学系统控制光通过的量的孔组,和形成图像的另一组。
由于传播的光波能在波列的角度来讨论,光线束可以通过定向正常的波阵面光线追迹来表示。 考虑到这一事实的考虑,在图4中讨论的双透镜系统可以降低到光线轨迹,如图2中所示的示意图中,为了应用几何结构的规则,以确定图像的大小和位置由透镜形成。 如上所讨论的,两个代表性光线一近轴(平行)于光轴,以及一个通过透镜的中心都是必要确定这些参数。
的距离a和b,如图2(F(a)和f(b)以图4)和后焦距(f)的透镜是由简单的等式在适用于所有的薄透镜彼此相关:
从这个等式中,显而易见的是,如果后焦距和透镜和物体之间的距离是已知的,则可以计算镜头和焦平面之间的距离。 此外,由透镜的对象的高度除以产生的图象的高度决定了透镜的横向放大率 (M):
当然,上面描述的等式基于该透镜系统由空气包围两侧的假设,但这种使用油,水,或甘油浸渍物镜时往往不是在光学显微镜的情况。 然而,大多数普通显微镜中低倍率的物镜的不使用除空气以外的成像介质。 在可以从刚刚讨论的简单透镜数学推导的结论是,图像的放大率(或缩小尺寸)等于透镜系统的焦距,由物体面和焦平面之间的距离除以在透镜的前侧(物体侧)。 除的图像,放大(或缩小)等于图像平面和在透镜的右侧焦平面,由透镜的焦距除以之间的距离。 这些方程通常用于放大或缩小图像的大小由具有固定焦距的透镜系统的计算。 它们还用于从所述主面确定在透镜的右侧(图象空间)侧的图像的距离,当试样被放置在对象空间中的固定距离是有用的。
即在显微镜重要的另一个因素是纵向或轴向放大,其被定义为距离的两个图像点之间沿透镜它们在检体对应的共轭点的轴的比值。 在一般情况下,纵向倍率的幅度是由在图像平面内小的距离的横向放大率的平方确定。
结论
能够形成图像(如双凸透镜)的单透镜是在设计用于简单放大的应用,如放大镜,眼镜,单镜头相机,放大镜,取景器,和隐形眼镜的工具是有用的。 最简单的双联(双透镜系统)被称为消色差镜头,并且由在为了校正轴上球形和色差胶合在一起的两个透镜元件。 消色差双合通常由耦合至一个正或负的弯月形透镜或一个平凸透镜的双凸透镜。 (含有三个透镜元件)三重峰消色差透镜被用作高倍率放大镜及中继透镜。 像差比双峰更高度纠正,三合透镜的组合通常是通过计算机设计技术进行了优化,以从根本上消除失真。 更复杂的装置常常采用多透镜组件的组合,以提高放大倍数,并采取图像的其它光学性能的优势。 这些包括显微镜,望远镜,潜望镜,照相机和望远镜,它们是使用复式光学系统的许多设备之间。

除了如上所述,镜片也产生在各种其它形状和尺寸的共同几何形状(见图5)。 球面球透镜从所有入射角显示出相等的属性,并具有只取决于直径和折射率的焦距。 通过操纵这两个变量,焦距的广谱可以与球透镜来实现,但它们的主要应用是提高纤维,发射器,并在电信行业利用探测器之间的信号耦合。 半球透镜,这是半球形,是在光纤通信光学,内窥镜,显微镜和激光测量系统是有用的。 鼓镜片从由消除透镜半径的显著一部分轴向研磨技术球透镜生产。 这些改性透镜更容易安装和对齐在比他们的球透镜对应的光学系统。
柱面透镜,其在各种各样的形状和尺寸所产生的,由展平在一个表面上的圆筒的一部分的在单一平面光聚焦。 因为这些透镜是能够放大在一个单一的方向上,它们可被用于拉伸图像。 此外,柱面透镜可以将点光源成线图像,使得它们可用作激光线发生器或光聚焦到一个缝隙。 其他透镜形状包括锥形 , 棒 ,和非球面光学元件。 锥形透镜用于360度的照明和图像处理应用程序。 具有类似于圆柱透镜的光学性能,棒状透镜将集中准直的光穿过直径成一条线。 非球面透镜,它可以在大量的各种数值孔径的产生,消除球差和改进聚焦和准直精度。 这些镜头通常被用在高效率的照明系统作为聚光镜的元件。
形成在显微镜的光学组件图像的光学部件是照射器(聚光镜)透镜,聚焦透镜(物镜),和目镜透镜。 虽然没有一般被描述为成像元件,这些单个透镜元件和组的成像特性是至关重要在确定由显微镜产生的图像的最终质量。