

- 您好,欢迎您访问成贯仪器官方网站!


许多透明固体是光学各向同性的,这意味着折射率在整个晶格的所有方向上相等。各向同性固体的实例是玻璃,食盐(氯化钠,如图1(a)所示),许多聚合物,以及各种有机和无机化合物。
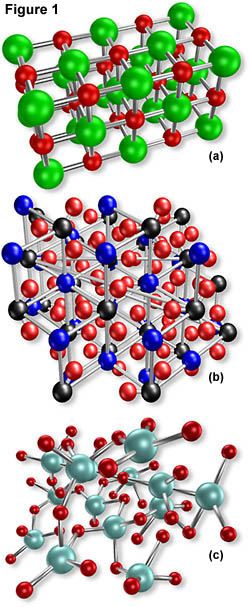
最简单的晶格结构是立方的,如图1(a)中氯化钠的分子模型所示,其中所有的钠离子和氯离子沿三个相互垂直的轴排列成均匀的间隔。每个氯离子被六个单独的钠离子包围(并静电结合),对于钠离子,反之亦然。图1(b)中所示的晶格结构代表矿物方解石(碳酸钙),其由钙和碳酸根离子组成。方解石具有各向异性晶格,其与光以与各向同性晶体完全不同的方式相互作用。图1(c)中所示的聚合物是无定形的并且没有任何可识别的晶体结构。
晶体被分类为各向同性或各向异性,这取决于它们的光学行为以及它们的晶轴是否相等。无论相对于入射光波的晶体取向如何,所有各向同性晶体具有以类似方式与光相互作用的等效轴。进入各向同性晶体的光以恒定角度折射并以单一速度通过晶体,而不会通过与晶格的电子元件的相互作用而极化。
另一方面,各向异性晶体具有结晶学上不同的轴,并且以取决于晶格相对于入射光的取向的方式与光相互作用。当光进入各向异性晶体的光轴时,其作用方式类似于与各向同性晶体的相互作用并以单一速度通过。然而,当光进入非等效轴时,它被折射成两条光线,每条光线以彼此成直角定向的振动方向偏振,并以不同的速度行进。这种现象被称为“ 双 ”或“ 双 ” 折射,并且在所有各向异性晶体中或多或少地看到。

如图2所示,碳酸钙(方解石)晶体可能是最具戏剧性的双折射演示。图2中方解石的菱形解理块在放置在蓝色铅笔上时产生两个图像。当您通过透明玻璃或各向同性晶体观察物体时,通常会出现其中一个图像。由于双折射光的性质,另一个铅笔图像看起来移位。当各向异性晶体折射光时,所产生的光线被极化并以不同的速度行进,如上所述。其中一条光线在每个方向上以相同的速度穿过晶体,被称为普通光线射线。另一条光线的移动速度取决于晶体内的传播方向。这种光线被称为非常光线。普通和非常光线之间的分离距离随着晶体厚度的增加而增加。各向异性晶体的两个独立折射率根据它们的双折射来量化,双折射是折射率差异的量度。因此,晶体的双折射(B,通常称为δ或Δ)定义为:
其中n high是最大折射率,n是低是最小的。除了沿晶体光轴传播的光波之外,该表达式适用于各向异性晶体的任何部分或片段。如上所述,通过各向异性晶体双重折射的光被偏振,偏振的普通和非常光波的振动方向彼此垂直取向。我们现在可以在偏光显微镜中检查各向异性晶体在偏振照射下的表现。图3示出了放置在两个偏振器之间的双折射晶体,所述两个偏振器的振动方向彼此垂直(并且根据偏振器和分析器标签旁边的箭头定向)。
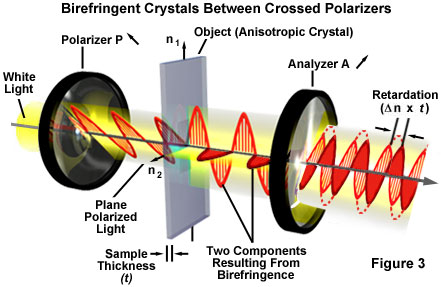
进入左侧偏振器的白光以箭头所示方向(偏振器标签旁边)的方向偏振,并且由“红色”正弦光波任意表示。接下来,偏振光进入各向异性晶体,在那里它被折射并分成两个独立的部件,它们平行于晶轴振动并彼此垂直(任意地,“蓝色”和“红色”光波)。然后,偏振光波通过分析仪(其偏振位置由分析仪标签旁边的箭头指示),该分析仪仅通过与分析仪的偏振方向平行的那些光波分量。,由各向异性晶体折射的普通和非常光线之间的速度差异。
现在让我们更仔细地研究双折射各向异性晶体如何在光学显微镜中与偏振光相互作用。我们的主题材料是假想的四方晶体,其光轴平行于晶体的长轴取向。从偏振器进入晶体的光将垂直于晶体的光学(长)轴行进。图4显示了在交叉偏振照射下在显微镜目镜中出现的晶体。在图4的每个部分中,显微镜偏振器的轴由P表示并且以东西方向定向。显微镜分析仪的轴用A表示并且朝向南北方向。这些轴彼此垂直,当通过目镜观察时,在没有插入双折射晶体的情况下产生完全暗场。图4(a)示出了各向异性双折射晶体,其具有平行于偏振器方向取向的长(光学)轴。
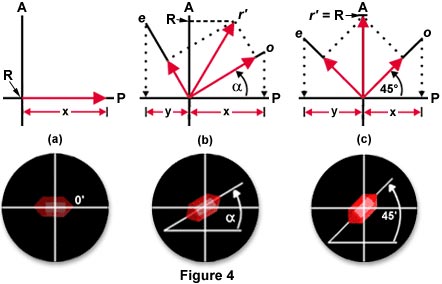
在这种情况下,穿过偏振器并随后穿过晶体的光在平行于偏振器方向的平面中振动。光通过分析仪没有贡献(因为光振动的单一方向 - 与偏振器平行)导致晶体非常暗且几乎不可见。在图4(a)中,晶体并非完全灭绝(因为它将在交叉偏振器之间),而是通过一小部分红光。这样做只是为了让参观者注意到水晶的位置。
显微镜学家经典地将这种取向称为晶体消光的位置。该观察对于用偏光显微镜确定各向异性材料的折射率是重要的。通过在交叉偏振显微镜中移除分析器,通过偏振器的光的单个允许振动方向仅与双折射材料(晶体)中的一个电子组件相互作用。这允许单个折射率的分离用于测量。然后可以通过将偏振器旋转90度来测量材料的剩余折射率。
图4(b)中的情况非常不同,其中晶体的长(光)轴现在相对于偏振器成一角度(α)。在这种情况下,通过偏振器接收的一部分光被传递到分析仪。为了定量通过分析仪的光量,我们可以应用简单的矢量分析来解决问题。第一步是找到偏振器对o和e的贡献(见图4(b)---这些是普通(o)射线和非常(e)射线的任意名称,类似于Foster描述的方法)。这是通过将矢量的投影下降到偏振器的轴上来实现的。对于o和e,该方法假设任意值为1 ,其与普通和非常光线的实际强度成比例。来自偏振器对o和e的贡献用在图4(b)中的偏振器轴(P)上由x和y表示的红色箭头示出。然后在矢量o和e上测量这些长度(在矢量上也显示为红色箭头)以产生合成的r',将其投射到分析仪轴上(A)作为绝对值ř。如上所述,分析仪轴上的R值与通过分析仪的光量成正比。这表明来自偏振器的一些光通过分析仪,双折射晶体显示出一定程度的亮度。
当晶体的长(光)轴与偏振器和分析器成45度角时,显示双折射材料的最大亮度,如图4(c)所示。将矢量o和e的投影下降到偏振器轴(P)上确定了偏振器对这些矢量的贡献。然后,当在矢量上测量这些投影时(再次使用矢量上的红色箭头)并完成矩形以计算结果值r',我们发现在该系统中对光通过的最大可能贡献。这种方法适用于任何晶体相对于偏振器和分析器轴的方向,因为o和e总是彼此成直角,唯一的区别是o和e相对于晶轴的方向。
为了进一步研究这种现象,我们邀请您访问我们的交互式Java教程,该教程探讨在偏振显微镜中在偏振器和分析器之间旋转时通过双折射晶体的光量。请使用Java文本框中的链接导航到本教程。
现在我们将考虑普通和非常光线穿过双折射晶体后的相位关系和速度差异。这些光线定向成使它们彼此成直角振动。每条射线在进入晶体时都会遇到稍微不同的电气环境(折射率),这将影响光线穿过晶体的速度。由于折射率的差异,一条光线将以比另一条光线慢的速率穿过晶体。换句话说,较慢射线的速度将相对于较快射线延迟。可以使用以下等式量化该延迟:
其中Γ是材料的定量延迟,t是双折射晶体(或材料)和B的厚度是如上定义的双折射。有助于延迟值的因素是普通和非常光线所见环境的折射率差异的大小以及样品厚度。显然,折射率或厚度的差异越大,延迟程度越大。对矿物方解石进行的早期观察表明,较厚的方解石晶体在通过图2中所示的晶体看到的图像的分裂中引起更大的差异。这与上面的等式一致,即状态延迟将随着晶体(或样品)厚度而增加。
当普通和非常光线从双折射晶体中出现时,它们仍然相对于彼此以直角振动。但是,通过分析仪的这些波的分量在同一平面内振动,如上图3所示。因为一个波相对于另一个波延迟,所以当波通过分析器时,在波之间发生干涉(建设性的或破坏性的)。最终结果是,当通过交叉偏振器在白光中观察时,一些双折射样品获得了一种颜色光谱。这将在偏振光显微镜部分中更详细地讨论。
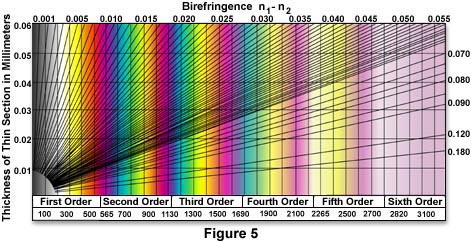
在双折射样品中看到的颜色的定量通常通过上面图5中所示的Michel-Levy图表来提供。从该图中可以明显看出,在显微镜中看到的偏振颜色可以与样品的实际延迟,厚度和双折射相关联。如果你知道三个变量中的两个,那么该图表很容易与双折射样本一起使用。当样品放置在显微镜中的交叉偏振器之间并旋转到最大亮度的位置时,样品产生的颜色可以在延迟轴上向下追踪,以找到样品的普通和非常光线之间的波长差异。或者,通过测量样品的折射率并计算它们的差异(双折射(B),您可以从图表顶部的双折射值中找到样本的颜色。通过将成角度的线外推回纵坐标,您还可以计算样本的厚度。
Michel-Levy图表的底部标记了延迟的顺序,大约为550纳米的倍数。零和550纳米之间的区域被称为偏振色的第一级,并且在550纳米区域中出现的品红色通常被称为一级红色。550到1100纳米之间的颜色被称为二阶颜色,依此类推。图表开头的黑色称为零级黑色。大多数Michel-Levy图表绘制了高阶颜色,直到五阶或六阶。
图表中最敏感的区域是一阶红色(550纳米),因为即使延迟的轻微变化也会导致颜色显着偏移,直至青色或黄色。许多显微镜制造商通过提供全波延迟板或一阶红色补偿器及其偏光显微镜来利用这种灵敏度,以帮助科学家确定双折射材料的特性。