

- 您好,欢迎您访问成贯仪器官方网站!


数值孔径(也称为对象侧孔径)是Abbe最初为显微镜物镜和聚光镜定义的值(通常由缩写NA表示)。它由简单的表达式给出:
数值孔径(NA)=n×sin(μ) 或 n×sin(α)
注意:许多作者使用变量μ来指定二分之一角孔径,而另一些作者则使用更常用的项α,在某些情况下使用θ。
在数值孔径方程中,n表示物镜前透镜与样品之间的介质的折射率,μ或α是物镜的二分之一角孔径。
显微镜物镜的数值孔径是其在固定的物距下收集光和分辨细小样品细节的能力的量度。形成图像的光波穿过样品并以倒圆锥形进入物镜,如图1所示(上图)。该光锥的纵向切片显示出角孔,该值由物镜的焦距确定。
数值孔径是物镜捕获的高衍射光线的量度。
在实践中,使用干物镜很难获得大于0.95的数值孔径值。图1展示了一系列从不同焦距和数值孔径的物镜得到的光锥。随着光锥的增大,角孔径(α)从7°增加到60°,结果数值孔径从0.12增加到0.87,接近将空气用作成像介质时的极限。通过增加成像介质的折射率(n)在样品和物镜前透镜之间。显微镜物镜现已上市,可以在其他介质中成像,例如水(折射率= 1.33),甘油(折射率= 1.47)和浸油(折射率= 1.51)。物镜的数值孔径在某种程度上还取决于光学像差的校正量。
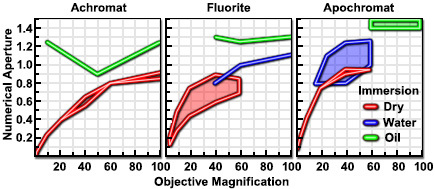
高度校正的物镜往往具有更大的数值孔径,如下面的图2和表1所示。如果我们以一系列典型的10倍物镜为例,可以看到对于平场校正的平场物镜,数值孔径的增加对应于色差和球差的增强校正:平场消色差,NA = 0.25;平场萤石,NA = 0.30; 平场复消色差,NA = 0.45。
如表1所示,在一系列类似放大倍率的物镜中,随着光学校正因子的增加而增加数值孔径的这一特性在整个放大倍率范围内都适用,大多数制造商都在努力确保其物镜具有最高的校正度和数值孔径。每个目标类别都有可能。
| 放大倍数 | 平常消色差(NA) | 平场萤石(NA) | 平场复消色差(NA) |
|---|---|---|---|
| 0.5倍 | 0.025 | 不适用 | 不适用 |
| 1倍 | 0.04 | 不适用 | 不适用 |
| 2倍 | 0.06 | 不适用 | 0.10 |
| 4倍 | 0.10 | 0.13 | 0.20 |
| 10倍 | 0.25 | 0.30 | 0.45 |
| 20倍 | 0.40 | 0.50 | 0.75 |
| 40倍 | 0.65 | 0.75 | 0.95 |
| 40倍(油) | 不适用 | 1.30 | 1.00 |
| 60倍 | 0.75 | 0.85 | 0.95 |
| 60x(油) | 不适用 | 不适用 | 1.40 |
| 100x(油) | 1.25 | 1.30 | 1.40 |
| 150倍 | 不适用 | 不适用 | 0.90 |
放大倍率范围在60倍至100倍(甚至更高)之间的大多数物镜都设计用于浸没油。通过检查上面给出的数值孔径方程,我们发现,普通浸油可获得的最高理论数值孔径为1.51(当sin(α)= 1时)。然而,实际上,大多数油浸物镜的最大数值孔径为1.4,最常见的数值孔径范围为1.0至1.35。
注意:除非在像侧指定,否则术语“数值孔径”是指物体侧。