

- 您好,欢迎您访问成贯仪器官方网站!


当电磁辐射以可见光的形式从一种物质或介质传播到另一种物质或介质时,光波可能会发生一种称为折射的现象,该现象通过光的弯曲或方向变化来体现。仅当两种材料之间的折射率存在差异时,光才会从一种介质传递到另一种介质,从而发生折射。折射的影响是造成各种常见现象的原因,例如部分浸入水中的物体的明显弯曲以及在炎热的沙质沙漠上观察到的海市蜃楼。可见光的折射也是镜头的重要特征,它使它们能够将光束聚焦到单个点上。

十九世纪初,花边制造商依靠充满水的玻璃球将烛光聚焦或聚集到工作的小区域,以帮助他们更清晰地看到细节。图1显示了1800年代制造的花边机的聚光器,该聚光器由数个玻璃球组成,这些玻璃球在烛台周围呈圆形排列,使来自蜡烛的光聚焦或集中到几个亮点。玻璃球的曲面充当光线的大收集面,然后以类似于凸透镜的方式朝着公共焦点折射。聚光镜或聚光镜也用于现代显微镜和其他光学仪器中,以像早期花边制造商的聚光镜一样依赖于折射原理来聚光。
当光从一种物质进入另一种物质时,它会直接越过两种物质之间的边界(垂直或90度入射角)而直接通过而不会改变方向。但是,如果光线以任何其他角度撞击边界,则它将弯曲或折射,并且随着光束相对于边界以更大的角度逐渐倾斜,折射程度会增加。例如,一束垂直射向水的光束不会发生折射,但是如果光束以很小的角度进入水中,则会被折射到很小的程度。如果光束的角度进一步增大,则光将与入射角成比例地折射。
几个世纪以来,人类注意到了一个相当奇怪但显而易见的事实。当一根直杆或棍棒部分浸入水中时,该杆不再显得笔直,而是以不同的角度或方向倾斜(请参见图2,这是用一杯水中的苏打水进行的这种效果的图示)。光线离开水时会发生折射,从而产生一种幻觉,即水中的物体看上去比实际扭曲而且靠近。图2中的吸管由于来自吸管表面的反射光波的折射而显得放大并且略微变形。波浪首先必须穿过水,然后穿过玻璃/水边界,最后穿过空气。来自吸管侧面(正面和背面)的光波比来自吸管中心的光波偏移程度更大
早在公元一世纪,古希腊的天文学家和地理学家托勒密就试图用数学方法解释所发生的弯曲(或折射)量,但后来他提出的定律被认为是不可靠的。1600年代,荷兰数学家Willebrord Snell成功地制定了一条定律,该定律定义了与入射角和折射角之比有关的值,该值随后被称为弯曲能力或折射率一种物质。实际上,物质能够使光弯曲或折射的越多,则其折射率值就越大。水中的棍棒似乎弯曲了,因为从棍棒反射的光线在到达我们的眼睛之前在空气-水界面处突然弯曲。令他失望的是,斯内尔从未发现这种折射效应的原因。

1678年,另一位荷兰科学家克里斯蒂安·惠更斯(Christiaan Huygens)设计了一种数学关系式来解释Snell的观察结果,并提出材料的折射率与光穿过该物质的速度有关。惠更斯确定,具有不同折射率的两种材料中与光路角度有关的比率应等于光通过每种材料时的传播速度比率。因此,他假定,光将通过具有较大折射率的材料传播得更慢。换句话说,通过材料的光速与折射率成反比。尽管此点已通过实验验证,对于缺乏可靠的方法来测量光速的大多数17世纪和18世纪研究者来说,这并不是立即显而易见的。对于这些科学家而言,无论光通过的材料如何,光似乎都以相同的速度传播。惠更斯逝世已有150多年了,光速的测量精度足以证明他的理论是正确的。
扩展先前的思想,将透明物质或材料的折射率定义为光在真空中穿过该材料的相对速度。按照惯例,真空的折射率定义为具有1.0的值,该值用作公认的参考点。通常由变量n标识的其他透明材料的折射率通过以下公式定义:
其中c是真空中的光速,v是材料中的光速。因为真空的折射率定义为1.0,并且光在真空中达到其最大速度(没有任何材料),所以所有其他透明材料的折射率都超过1.0的值,并且可以通过技术数量。对于大多数实际目的,空气(1.0003)的折射率非常接近真空的折射率,因此可以用来计算未知材料的折射率。表1列出了几种常见的透明材料的折射率测量结果。具有较高折射率的材料比具有较低折射率的材料在更大程度上降低了光速。实际上,据说这些材料具有更高的折射性,
| 材料 | 折射率 |
|---|---|
| 空气 | 1.0003 |
| 水 | 1.333 |
| 甘油 | 1.473 |
| 浸油 | 1.515 |
| 玻璃(皇冠) | 1.520 |
| 玻璃(火石) | 1.656 |
| 锆石 | 1.920 |
| 钻石 | 2.417 |
| 硫化铅 | 3.910 |
当光波从折射率较低的介质(例如空气)传播到折射率较高的介质(例如水)时,波速降低。相反,当光从折射率较高的介质(水)传播到折射率较小的介质(空气)时,波速增加。在正常定义为垂直于两种物质之间的边界或界面的线。相对于法线的第一介质的入射角和相对于法线的第二介质的折射角(也相对于法线)将与两种物质之间的折射率差异成比例地不同。如果光波从折射率较低的介质传递到折射率较高的介质,则它会朝法线方向弯曲。但是,如果波从折射率较高的介质传播到折射率较低的介质,则它会偏离法线。 斯涅尔定律将两种光波的角度与两种材料的折射率之间的关系描述为:
在斯涅尔方程中,变量n(1)表示入射光线在其中传播的介质的折射率,而n(2)是折射光线在其中传播的介质的折射率。值θ(1)表示入射光线撞击边界的角度(相对于法线),而θ(2)是折射光线传播的角度。
从斯涅尔方程可以得出几个重要点。当n(1)小于n(2)时,折射角始终小于入射角(向法线弯曲)。或者,当n(2)小于n(1)时,折射角始终大于入射角(远离法线弯曲)。当两个折射率相等时(n(1) = n(2)),则两个角度也必须相等,从而使光通过时不会发生折射。
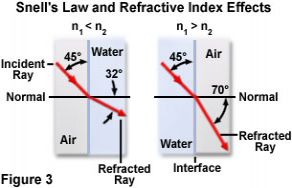
图3说明了上述两种情况,其中n(1)大于n(2),n(1)小于n(2),且入射角为45度。介质由空气和水组成,折射率分别为1.000和1.333。在图3的左侧,穿过空气的光波以45度角入射到水表面,并在与法线成32度角进入水中时发生折射。当情况相反时,在水中具有相同入射角的光线在进入空气时会以70度角折射。
斯涅尔定律重新排列为另一种形式,证明了入射角和折射角的正弦之比等于常数n,它是两种介质中光速(或折射率)的比率。该比率n(2)/ n(1)被称为这两种物质的相对折射率。
折射率概念的另一个方面在下面(图4)进行了说明,其中光束从空气穿过玻璃和水,然后重新进入空气。请注意,虽然两个光束相对于法线(60度)都以相同的入射角进入折射率更高的材料,但由于玻璃的折射率较高,玻璃的折射率比水的折射率大约大6度。
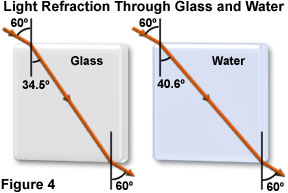
光束在进入时折射,并且在离开较高折射率的材料时再次折射,沿与入射路径相反的方向折射。两种光束都以与入射时相同的角度出射,但是出射点沿边界横向移动,这是因为光束在穿过两种较高折射率的材料时,所采用的角路径不同。折射的这种影响在镜头设计中对于控制成像光线的精确焦点非常重要。
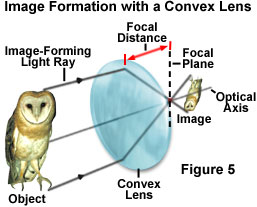
光的折射是透镜物理的一个重要方面,尤其是在如何设计和构造单透镜或多透镜系统方面。在简单的凸透镜中,从物体反射的光波被透镜收集并向光轴折射,以会聚在后焦点上(图5)。物体相对于镜头前焦点的相对位置决定了物体成像的方式。如果物体的位置超过焦点到镜头的距离的两倍,则该物体看起来更小且倒置,并且必须用附加的镜头成像才能放大尺寸。但是,当物体比前焦点更靠近镜头时,图像看起来像是竖直且更大,这可以通过简单的放大镜轻松地看到。
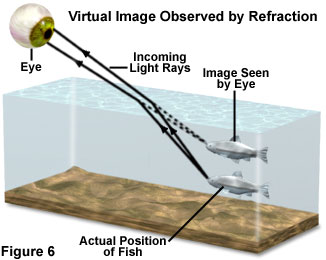
在日常生活中通常会观察到许多由光折射引起的现象。几乎每个试图伸手摸摸淹没在水中的东西的人,最常见的经历之一。由于光线从水中传播到空气中时会发生折射,因此水中出现的物体通常看起来与实际深度不同。眼睛和大脑将光线追溯到水中,就好像它们没有折射一样,而是从物体沿直线传播,从而创建了一个物体的虚像,并以较浅的深度出现。
从湖泊或池塘的岸边观察时,鱼在浅水中的实际深度的错觉由折射效应产生的错觉很好地说明了这一概念(见图6)。当我们注视着水面观察鱼在池塘周围游泳时,它们看起来比实际位置更接近水面。另一方面,从鱼的角度来看,由于反射和透射的光到达鱼眼后折射而产生的虚像,整个世界在水面上方显得扭曲和压缩。实际上,由于折射,河岸上的渔夫似乎比他或她更远离鱼(从鱼的角度来看)。
该现象可用于通过光学显微镜确定液体的折射率。为了进行此实验,构造(或购买了)一个能够容纳带有标记(或刻度)的液体的扁平电池,该标记位于玻璃内部表面上。显微镜目镜中的一个必须在主像平面上插入有刻度的标线片,以便测量扁平单元中标记的线宽。在将未知折射率的液体添加到样品池之前,将显微镜聚焦在样品池底部的标记上,并记录下标记在标线板上的位置。接下来,将少量液体添加到细胞中,并将显微镜重新聚焦在标记上(通过液体),然后进行新的测量。显微镜最终聚焦在液体表面,然后通过测量掩模版上标记的位置来记录第三次读数。然后可以使用以下公式计算未知液体的折射率:
其中D(实测)是使用显微镜测得的深度(从液体表面到标记在空细胞上的位置),D(表观)是有或没有液体时的标记测量值。
尽管通常必须使光从一种物质进入另一种物质才能发生折射,但是在某些情况下,诸如温度梯度之类的扰动会在单一介质内产生足够的折射率波动,从而产生折射效果。如果它们具有明显不同的温度,则大气中重叠的空气层会产生通常称为海市蜃楼的现象,即观察到物体的虚像位于实际物体上方或下方的现象。
较冷和较冷的空气分层在沙漠地区,海洋和热沥青路面(如停车场和高速公路)上尤为常见。可视化的实际海市蜃楼效果取决于冷空气是否覆盖热空气,反之亦然(图7(a))。海市蜃楼的一种形式是位于真实物体正下方的倒置虚拟图像,当地面或水面附近的一层暖空气被上方较冷的较冷空气困住时,就会发生。来自物体的光向下传播到与地面相邻的温暖的空气中(或水),朝着地平线向上折射。在某个时刻,光达到暖空气的临界角,并通过全内反射向上弯曲,从而导致虚像出现在物体下方。

海市蜃楼的另一种形式称为“ 隐约可见”,发生在温暖的空气覆盖在较冷的空气上时,这种现象普遍存在于大型水域中,当白天加热水上方的空气时,这些水域可能保持相对凉爽(参见图7(b) ))。来自物体(例如,水面上的船)的光线通过冷空气向上传播到较热的空气中,并向着观察者的视线向下折射。然后,光线似乎是从对象上方发出的,并且似乎“隐约可见”于其实际位置上方。通常,地平线附近海上的船舶似乎漂浮在水面之上。
可见光波长色散
尽管通常参考物质的标准和固定折射率,但是仔细的测量表明,特定材料的折射率会随辐射的频率(和波长)或可见光的颜色而变化。换句话说,物质具有许多折射率,这些折射率可能随光的颜色或波长变化而略有不同或相差很大。几乎所有透明介质都会发生这种变化,因此被称为分散。特定材料表现出的色散程度取决于折射率随波长变化多少。对于任何物质,随着光波长的增加,折射率(或光的弯曲)会降低。换句话说,包括可见光中最短波长区域的蓝光以比具有最长波长的红光大得多的角度折射。普通玻璃的光散射是棱镜熟悉地将光分解成各种颜色的原因。
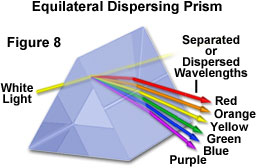
十七世纪末,艾萨克·牛顿爵士进行了一系列实验,从而发现了可见光谱,并证明了白光是由一种有序的颜色组成的,这些颜色从一端开始是蓝色,一直到绿色,黄色。和橙色,最后在另一端以红色结尾。牛顿在一个昏暗的房间里工作,将玻璃棱镜放在狭窄的阳光前,该阳光从钻入百叶窗的孔中射出。当阳光穿过棱镜时,有序的光谱被投影到位于棱镜后面的屏幕上。
牛顿从该实验得出的结论是,白光是由多种颜色的混合物产生的,并且棱镜通过将每种颜色以不同的角度折射从而使它们易于分离(图8),从而使白光扩散或“分散”。牛顿无法进一步细分各个颜色,他尝试通过将单色分散光通过第二个棱镜来进行尝试。但是,当他将第二个棱镜放置在非常接近第一个棱镜的位置时,所有分散的颜色都进入了第二个棱镜,牛顿发现这些颜色会重新组合以再次产生白光。这一发现提供了确凿的证据,即白光由可以轻松分离和重新组合的多种颜色组成。
色散现象在各种常见观察中起着至关重要的作用。当阳光被落在大气中的雨滴折射时,会形成彩虹,从而产生壮观的光谱颜色显示,与棱镜显示的光谱颜色非常相似。此外,由精美切割的宝石(如钻石)产生的闪闪发光的色彩是由白光产生的,这些白光被精确成角度的小面折射和散射。
在测量透明物质的折射率时,必须确定测量中使用的特定波长。这是因为色散是与波长有关的现象,并且测得的折射率将取决于用于确定的光的波长。表2对可见光在各种介质中的散布进行了分类,如三种不同波长(或颜色)的光的折射率变化所示。
| 材料 | 蓝色 (486.1 nm) | 黄色 (589.3 nm) | 红色 (656.3 nm) |
|---|---|---|---|
| 皇冠玻璃 | 1.524 | 1.517 | 1.515 |
| 火石玻璃 | 1.639 | 1.627 | 1.622 |
| 水 | 1.337 | 1.333 | 1.331 |
| 嘉吉油 | 1.530 | 1.520 | 1.516 |
| 二硫化碳 | 1.652 | 1.628 | 1.618 |
用于测量折射率值的最常用波长是由钠灯发出的,钠灯具有牢固且紧密间隔的双峰,平均波长为589.3纳米。此光称为D线光谱,代表表2中列出的黄光。同样,F线和C线光谱对应于氢发出的特定波长的蓝光和红光(也在表2中列出)。从表中给出的值可以看出,将光的波长从486.1纳米(蓝色或F线)增加到656.3纳米(红色或C线)会导致特定介质的折射率明显降低。可以使用黄色,蓝色和红色光的三种特定波长来定量定义色散,如下所示:
其中n是材料在由D,F和C表示的特定波长下的折射率,它们表示钠和氢的光谱线,如上所述(请参见表2)。许多因素在各种材料的色散值中起关键作用,包括元素和分子组成以及晶格形态。几种无机固体具有非常高的分散性,包括铬酸盐,重铬酸盐,氰化物,钒酸盐和卤化物络合物。当掺入某些材料中时,有机取代基也可导致高分散值。
色散还造成色差,色差是由折射率随波长变化而导致的透镜伪像。当白光通过一个简单的凸透镜时,几个焦点会非常接近地出现,这对应于分量波长的较小折射率差异。这种效果往往会在对象的图像周围产生彩色的光晕(取决于焦点,是红色还是蓝色)。通过使用两个或更多个由具有不同色散特性的材料构成的透镜元件的组合来完成该像差的校正。一个很好的例子是同时使用冠和火石玻璃两个单独的元件构成的消色差双合透镜系统。
临界反射角
光学显微镜的一个重要概念是反射的临界角,这是选择使用干式或油浸式物镜以高倍查看样品时必须考虑的必要因素。当通过较高折射率的介质进入较低折射率的介质时,光波所采取的路径由相对于两种介质之间边界的入射角确定。如果入射角增加到超过特定值(取决于两种介质的折射率),则该入射角将到达一个角度很大的点,从而没有光被折射到折射率较低的介质中,如图9所示。在此图中,各个光线由从较高折射率(n(2))的介质向较低折射率(n(1)的介质之一)移动的红色或黄色箭头表示)。每个单独光线的入射角由值i表示,折射角由变量r表示。四个黄色光线的入射角(i)都足够低,以允许它们穿过两种介质之间的界面。但是,两条红色光线的入射角超过了临界反射角(对于水和空气示例,大约为41度),并且被反射到介质之间的边界中或反射回更高折射率的介质中。
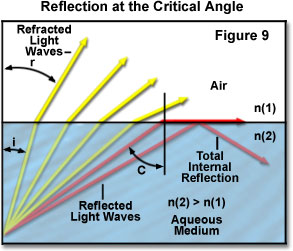
临界角现象发生在折射角(图9中的角r)等于90度且斯涅尔定律减小为:
其中(θ)现在被称为临界角(由变量表示Ç)。如果折射率较小的介质是空气(n = 1.00),则该方程式简化为:
当特定的光波超过临界角时,它将显示出全内反射回到介质中。通常将折射率较高的介质视为内部介质,因为在大多数情况下,空气(折射率为1.0)是周围介质或外部介质。当试图用盖玻片和物镜前透镜之间的空气以外的其他介质对标本成像时,此概念在光学显微镜中尤为重要。最常见的浸入介质(空气除外)是特种油,其折射率等于物镜前透镜和盖玻片所用玻璃的折射率。
从显微镜,望远镜到摄像机,电荷耦合器件(CCD),视频投影仪乃至人眼的光学设备,都从根本上依赖光可以被聚焦,折射和反射的事实。光的折射会产生各种各样的现象,包括海市蜃楼楼,彩虹和奇特的错觉,例如使鱼看起来比实际在浅水中游泳。折射还会使厚壁的啤酒杯看起来比实际的更饱满,并且欺骗我们以为太阳落山比实际时间晚了几分钟。数以百万计的人使用屈光力通过眼镜和隐形眼镜矫正错误的视力,使他们能够更清楚地看到世界。通过了解光的这些属性以及如何控制它们,