

- 您好,欢迎您访问成贯仪器官方网站!


通过等边棱镜的可见白光会经历一种称为色散的现象,这表现为光波的波长相关折射。这个交互式程序探讨了进入棱镜的白光的入射角如何影响色散度和离开棱镜的光的角度。
本程序初始化让白光以40度角入射到等边棱镜的单个面上,与从棱镜面绘制的垂线成40度角。为了改变入射角,使用鼠标光标平移入射角滑块,这也会产生棱镜分散的光线的出射角 (θ(d)) 的相应变化。的折射率滑块可以用于变化的1.40和2.00的值之间的棱镜折射率,增加由棱镜折射的光线的出射角。
1600 年代后期,英国物理学家艾萨克·牛顿爵士首次演示了三棱镜中的折射和色散。牛顿表明,可以通过具有相等边和角的等腰棱镜将白光分解成其组成颜色。通常,折射或色散棱镜具有两个或更多个平面,这些平面以有利于折射而不是反射入射光束的方式取向。当光线照射到色散棱镜的表面时,根据斯涅尔定律,光线进入时会发生折射,然后穿过玻璃,直到到达第二个界面。光线再次被折射并沿着新路径从棱镜射出(见图1)。因为棱镜改变了光的传播方向,据说穿过棱镜的波会偏离一个特定的角度,这可以通过将斯涅尔定律应用于棱镜的几何形状来非常精确地确定。当光波以允许光束在平行于底座的方向穿过玻璃的角度进入棱镜时,偏离角最小。
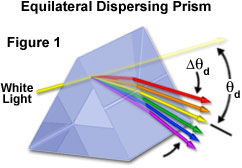
棱镜的光偏差量是入射角、棱镜顶(顶)角和构成棱镜的材料的折射率的函数。随着棱镜折射率值增加,通过棱镜的光的偏角也增加。折射率通常取决于光的波长,较短波长(蓝光)比较长波长(红光)以更大的角度折射。这种偏离角随波长的变化称为色散,并且是牛顿在 300 多年前观察到的现象的原因。通过为特定应用选择具有适当折射率特性的玻璃,可以微调色散。通常,各种玻璃配方的色散特性通过阿贝数进行比较,阿贝数是通过测量穿过玻璃的特定参考波长的折射率来确定的。