

- 您好,欢迎您访问成贯仪器官方网站!


显微镜物镜的数值孔径是其聚集的光,并在一个固定的物体距离解决细标本细节能力的量度。 图像形成光波穿过试样和如图1所示的该锥形光的纵切片示出孔径角,是由物镜的焦距确定的值中的倒置锥体进入物镜。
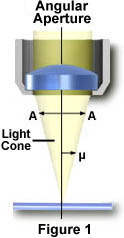
角μ是二分之一的孔径角(A)和涉及通过以下公式的数值孔径:
其中n是物镜的前透镜和样品盖玻璃,即从1.00范围为空气至1.51专门浸没油一个值之间的成像介质的折射率。 许多作者用变量α为μ数值孔径公式所示。 从这个方程很明显,当成像介质为空气(具有折射率,n = 1.0),则数值孔径仅取决于角度μ的最大值为90°。 角μ的sin,因此,具有(使用“干”显微镜物镜)的1.0(sin(90°)= 1),这是用空气作为成像介质操作透镜的理论最大数值孔径的最大值。
在实践中,但是,它是很难达到0.95以上的数值孔径值与干物镜。 图2示出了一系列从变焦距和数值孔径的物镜导出的光锥。 作为锥改变光的角度为7°μ增加,如图2(a)至图2的(c)60°,在数值孔径从0.12至0.87所得的增加,接近限制时空气是成像中。
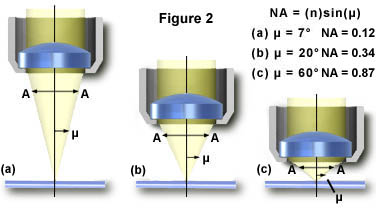
通过检查数值孔径方程,很明显,折射率是在实现数值孔径大于1.0的限制因素。 因此,为了获得更高的工作数值孔径,物镜的前透镜和试样之间的介质的折射率必须增加。 显微镜物镜现在可以允许成像另类媒介,例如水(折射率= 1.33),甘油(折射率= 1.47),和浸油(折射率= 1.51)。 护理应符合这些物镜被用于防止当一个物镜是用比它的物镜是为不同的液浸介质中使用,这将产生不希望的伪影。 我们建议显微镜从不使用专为浸油或者用甘油或水的物镜,虽然有几个新的物镜,最近出台了将与多个媒体合作。 你应该向制造商咨询是否有任何怀疑。
在60X和100X(或更高倍率)的放大倍率范围最物镜是设计用于浸油的使用。 通过检查上面的数值孔径方程,我们发现,与浸油得到的最高理论数值孔径为1.51(当sin(μ)= 1)。 在实践中,然而,大多数油浸物镜为1.4的最大数值孔径,以最常用的数值孔径为1.0到1.35。
物镜的数值孔径也依赖,在一定程度上,在校正光学象差的量。 高度校正的物镜趋于如下表1所示,以具有更大的数值孔径为各个放大倍数。 如果我们采取了一系列典型的10倍物镜为例,我们看到,平场校正的平场物镜,数值孔径增加对应校正色差和球面像差:平场消色差,NA = 0.25; 平场萤石,NA = 0.30; 并平场复消色差透镜,NA = 0.45。
| 放大倍率 | 消色差 (NA) | 萤石 (NA) | 复消色差 (NA) |
|---|---|---|---|
| 0.5X | 0.025 | N / A | N / A |
| 1X | 0.04 | N / A | N / A |
| 2X | 0.06 | N / A | 0.10 |
| 4X | 0.10 | 0.13 | 0.20 |
| 10X | 0.25 | 0.30 | 0.45 |
| 20X | 0.40 | 0.50 | 0.75 |
| 40X | 0.65 | 0.75 | 0.95 |
| 40X(油) | N / A | 1.30 | 1.00 |
| 60X | 0.75 | 0.85 | 0.95 |
| 60X(油) | N / A | N / A | 1.40 |
| 100X(油) | 1.25 | 1.30 | 1.40 |
| 150X | N / A | N / A | 0.90 |
示于表中的一系列类似倍率物镜跨越增加光学校正因子增加数值孔径的该特征保持在整个放大率范围内真正1.大多数制造商努力确保其物镜有最高的校正和数值孔径是可能为每个类的物镜。
显微镜物镜的分辨率被定义为仍然可区分为两个独立的实体的检体的两个点之间的最小距离。 分辨率是显微镜,因为在高放大倍率,图像可能会出现不清晰的,但仍然有点主观价值解析为物镜的最大能力。 数值孔径确定一个物镜的分辨能力,但在显微镜系统的总分辨率也取决于载物台聚光的数值孔径。 在整个系统的数值孔径越大,分辨率越高。
显微镜光学系统的正确对准是非常重要的还以确保最大的分辨率。 载物台聚光镜必须相对于数值孔径和孔径光阑为准确的光锥形成的调整相匹配的物镜。 用于图像的检体的光的波长谱也是第一个决定性因素。 比是较长波长更短的波长是能够解决的细节在更大的程度的。 有已被衍生来表达的数值孔径,波长,和分辨率之间的关系数方程:
| R =λ/ 2NA | (1) |
| R =0.61λ/ NA | (2) |
| R =1.22λ/(NA(Obj)+ NA(cond)) | (3) |
其中R是分辨率(两个对象之间的最小可分辨的距离),NA等于数值孔径,λ等于波长,NA(Obj)等于物镜的数值孔径,和NA(cond)是聚光镜的数值孔径。 注意,等式(1)和(2)通过乘法因子,这是0.5公式(1)和0.61方程不同(2)。 这些方程是基于许多因素(包括各种光学物理学家制成理论计算的)来解释的物镜和聚光镜的行为,并且不应当被认为任一项一般物理定律的绝对值。 在一些情况下,如共焦和荧光显微镜,分辨率实际上可能超过置于由这三个方程中的任何一个的限制。 其他因素,如低标本对比度和不当照明可以用于降低分辨率和,往往不是R(使用550纳米的中间光谱波长约0.25 微米 )的现实世界的最大值和的数值孔径1.35至1.40在实践中并未实现。 表2提供的列表的分辨率(R)和数值孔径(NA)由物镜放大倍率和纠正。
| 类型 | ||||||
| 平场消色差 | 萤石平场 | 平场复消色差透镜 | ||||
| 放大 | 数值孔径 | 分辨率 (微米) | 数值孔径 | 分辨率 (微米) | 数值孔径 | 分辨率 (微米) |
| 4X | 0.10 | 2.75 | 0.13 | 2.12 | 0.20 | 1.375 |
| 10X | 0.25 | 1.10 | 0.30 | 0.92 | 0.45 | 0.61 |
| 20X | 0.40 | 0.69 | 0.50 | 0.55 | 0.75 | 0.37 |
| 40X | 0.65 | 0.42 | 0.75 | 0.37 | 0.95 | 0.29 |
| 60X | 0.75 | 0.37 | 0.85 | 0.32 | 0.95 | 0.29 |
| 100X | 1.25 | 0.22 | 1.30 | 0.21 | 1.40 | 0.20 |
| NA =数值孔径 | ||||||
当在显微镜是在完美对准,并具有与载物台聚光镜适当匹配的物镜,那么我们就可以代替物镜的数值孔径为等式(1)和(2),与添加的结果是等式(3)简化为方程式(2)。 要注意的一个重要的事实是,倍率不会显示为在任何这些方程的一个因素,因为只有数值孔径和照明光的波长确定样品分辨率。 正如我们所提到的(并且可以在公式中看到)的光的波长是在显微镜的分辨率的一个重要因素。 较短波长产生更高的分辨率(对于R值越小),反之亦然。 在光学显微镜的最大分辨能力,实现与近紫外光,最短有效成像波长。 近紫外光后跟蓝色,然后绿色,最后红光在解决标本细节的能力。 在大多数情况下,显微镜使用由钨 - 卤素灯泡产生白光照亮样品。 可见光光谱在约550纳米,对于绿色光的主要波长为中心(我们的眼睛对绿光最为敏感)。 它是该波长的是使用在表2中的数值孔径值,计算分辨率值也是在这些方程和更高的数值孔径重要还会产生较高的分辨率,如表2明显的光的波长的效果上的分辨率,在一个固定的数值孔径(0.95),列于表3中。
| 波长 (纳米) | 分辨率 (微米) |
|---|---|
| 360 | 0.19 |
| 400 | 0.21 |
| 450 | 0.24 |
| 500 | 0.26 |
| 550 | 0.29 |
| 600 | 0.32 |
| 650 | 0.34 |
| 700 | 0.37 |
当来自样品的各个点光穿过物镜和复原为图像,检体的各个点显示图像作为称作艾里型态小图案(未分)英寸 这一现象是由衍射或光散射,因为它穿过在试样的微小部件和间隔和物镜的圆形后面孔引起的。 艾里图案的中央最大常被称作艾里斑 ,这被定义为通过艾里图案的第一最小值包围的区域,并且包含的光能量的84%。 这些艾里斑由小同心轻和黑眼圈的,如图3所示。该图显示了艾里磁盘及其强度分布作为间隔距离的函数。
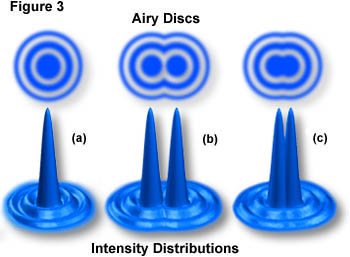
图3(a)示出一个假想艾里斑基本上由包含中央最大的衍射图案的(通常是零阶最大称为)由同心的第一,第二,第三,等,依次递减亮度的顺序最大值构成包围的强度分布。 两个艾里斑,并在光学分辨率的极限它们的强度分布在图3中(b)所示。 在图的这一部分,在两个盘之间的间隔超过其半径,并且它们是可解析的。 在其中两个艾里斑可以分解成独立的实体的限制通常被称为瑞利准则 。 如图3(c)示出了两个艾里斑,并在这样一种情况:零阶最大值之间的中心至中心的距离小于这些最大值的宽度它们的强度分布,并且两个磁盘不单独由瑞利准则解析。
在通过一个物镜在形成图像时,即成为可辨别样品的更详细的投影的艾里斑小。更高的校正(萤石和复消色差)的物镜产生更小的艾里斑比要低,校正物镜。 以类似的方式中,具有较高的数值孔径物镜也能够产生更小的艾里斑的。 这是高数值孔径和光学像差总校正的物镜可以在检体区分更精细的细节的首要原因。
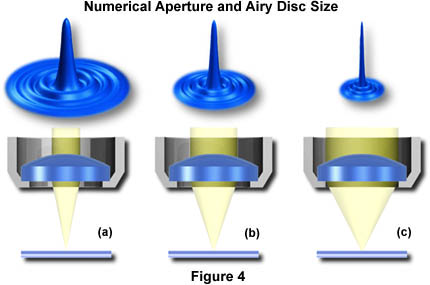
图4示出的数值孔径对具有一系列相同焦距的假想物镜成像艾里斑的大小的影响,但不同的数值孔径。 与小数值孔径,艾里斑的大小是大的,如图4(a)中。 作为物镜的增加的数值孔径和光锥角然而,如在图4(b)和图4(c)所示的艾里斑的大小减小。 在目镜膈肌水平产生的图像实际上是我们所认为的光明与黑暗的艾里磁盘的马赛克。 其中,两个磁盘靠得太近,使得它们的中心斑点重叠很大,由这些重叠磁盘表示的两个细节都没有解决或分离并因此显示为一个,如在图3的上方示出。
在图像形成理解一个重要的概念是由物镜截取衍射光线的性质。 仅在较高的(第一,第二,第三等)衍射光的订单被捕获的情况下,可以干扰工作重新创建在物镜的中间像平面的图像。 当只有零级光线被捕获,这几乎是不可能重构的试样的识别图像。 当一阶的光线被添加到零阶射线,图像变得更加连贯,但它仍然是足够的细节缺乏。 只有当高阶射线复合,该图像将代表样品的真实结构。 这对于大数值孔径(以及随后的更小的艾里斑)的必要性,以实现高清晰度图像,用光学显微镜的基础。
在一天到一天的例行观察,大多数显微镜不要试图达到的最高分辨率图像可能的他们的设备。 它只有在专门情况下,例如高倍率明场,荧光,DIC和共聚焦显微镜,我们力争达到显微镜的极限。 在显微镜的大多数用途,这是没有必要使用高数值孔径的物镜,因为试样容易与使用较低数值孔径物镜解决。 因为高数值孔径和高放大倍数都伴随着场的很浅深度(这指的是良好的聚焦在区域的正下方或正上方的区域被检查)和工作距离短的缺点,这是特别重要的。 因此,在标本,其中分辨率为不太重要的和放大倍数可以更低,最好是使用温和的数值孔径较低倍物镜以得到具有多个工作距离和更多的景深图像。
载物台聚光器孔径光阑的仔细定位也是数值孔径和不加区别地使用这种膜片可以导致图像质量下降(如在上一节讨论的控制关键载物台聚光镜 )。 其他因素,例如对比度和照明的效率,也影响图像分辨率的关键要素。